福田の雑談・思うこと

三角形の1つの頂点Aから対辺に向かって垂線AHを落とす問題。これを反射的にBH:HC=t:1-tと置いてしまう人は要注意！ そもそもHが辺BCを内分するかどうかわからないじゃないか！たまたま○になっただけかもよ。 解説動画を見る

「解き方を丸暗記しています」と言う人が結構います。でも本当の意味で理解していないと結局大切なときに使えないことになります。 用は「なぜそう考えたくなったか？」その気持ちを理解しない限り真の力にはなり得ない。 この問題の場合、「10で割り切れる」という表現をどう分解して考えるか、その過程の中で自然と余事象を考えたくなるはず。 そこら辺の心の動きを動画内で解説しています。 解説動画を見る

良問です。平行六面体を対角線の周りに１回転してできる立体の体積を誘導形式で求める問題。この平行六面体を対角線に垂直に3等分すると、 正四面体＋正八面体＋正四面体の３つに分かれるという話。 真ん中の図形が正八面体であることに気付くのは必須ではないのですが、気付いたときの喜びは大きいと思う。 気付けば、この部分の切り口が六角形であることも自明。回転半径も理解できます。 解説動画を見る

平面幾何の問題です。三角比、三角関数を上手に使えば、そんなに難しくはありませんが、プロセスが悪いとかなり大変な計算が必要になります。 本番では少々大変でもやりきる計算力が必要ですが… ただ、毎度毎度遠回りしながら力づくで解いてしまう生徒もいて、それはそれで尊敬はするのだけれど損してるなーとも思うわけですよ。 時には解けただけで満足せずに別の解法も学んで欲しいですね。 解説動画を見る

これは悪問と言わざるを得ません。設問(d)において接線が1本しか存在しないaの値を求める問題がありますが、接点の個数と接線の本数が 必ずしも一致しないことを気にせずに接点の個数だけで答を出した人も正解になるのはちょと… こういう問題を穴埋め形式で出題しないでもらいたい。記述形式なら答が合っていても減点したり0点にしたりできますが、 穴埋めでは「わかっていない人」の答が正解扱いになってしまいます しかもこの問題、接点の個数と接線の本数が一致することを示すのがかなり難しい問題です。その示し方も丁寧に解説しました。 記述対策に役立ててください。それにしてもボリュームのある問題だ。 解説動画を見る

前半の問はyを消去すればxに関する２次方程式の実数解条件を考える簡単な問題になります。後半は「少なくとも1つ0以上の解をもつ」条件を考える問題、 いわゆる解の配置問題、解の分離と呼ばれる類いの問題。 「少なくとも1つ0以上」と言われると面倒くさい場合分けが必要になりますね。グラフを利用する方法、 解と係数の関係を利用する方法など計３通りの解法を紹介しますので参考にしてください。 解説動画を見る

第１問は小問3題構成だが、どの問もボリュームがあった。その後の第２問、第３問も難易度が高く計算量も多いので受験生にはかなり大変なセットだったと思う。 それだけに第１問はどの問も解ききりたいよね。 勝負になるのは(c)(d)の２題だろう。(c)は二項係数の和に関する等式の証明問題で同じような経験をした人が多いのではなかろうか。 それに気付けば解ける。(d)はド・モアブルの定理を使えば早く計算できる。 解説動画を見る

最初にさいころの3回の目が3の倍数になる確率を求めるのだが、これに何の意味があるのか？を考えるべき。 そのためには目の積が3の倍数の時、何が起こるのかを調べることだね。続きは解説の中で。 解説動画を見る

焦点と準線、離心率を与えて、軌跡の方程式を求める問題。焦点？準線？離心率？？？などと身構えなくても大丈夫。そんなこと知らなくてもこの問題は解けます。 ただ、これらの背景をわかっていれば見通しはよくなります。 この問題のポイントは与えられた点Ｐの軌跡を極方程式で表すところかな。 ２次曲線は焦点の１つを極に置くと極方程式が表しやすいことは教科書にも載っていると思うので見直しておこう。 解説動画を見る

これはよい問題。与えられた方程式の異なる実数解の個数を調べる問題です。与えられた式を与えられたままで見ているだけではなく、同値変形して扱いやすい形になおしてから考える。 これは難問に対する姿勢としてとても大切なことです。 この問題をやるときには、問題の最初の所だけを読んで挑戦してください。穴埋めを始めるとせっかくの考える機会を失ってしまいます。 いいですか、絶対問題の誘導を見ないで解いてくださいね。 解説動画を見る

無限等比級数の和のさらに極限を計算する問題です。この無限級数が少し見にくい形をしているので等比級数であることを認識するのに時間がかかる人も… そんなときはΣを使わずに書き並べるのも一つの手ですよ。 解説動画を見る

定積分の極限を求める問題。問題は定積分の部分をどう見るか？logやsinが混じっていて しかも絶対値もついている嫌な式ですがそういう余計な情報を削って骨組みだけを見ていくと突破口が開けますよ。 解説動画を見る

簡単な問題ですが、答が合うかどうかだけでなくグラフがちゃんと描けたか？与えられた関数のグラフは正弦曲線であることがわかっているか？をチェックしましょう。 それが別の場面で役に立つかもしれませんよ。 解説動画を見る

数Ⅲの無限級数の問題でよくある図形への応用問題ですが、文系の人は不慣れな人が多くて大変だったかも。 帰納的に定義された規則を考えるときn番目とn+1番目の関係を考えるという概念に慣れておかないとね。 結局、連立漸化式を解く問題になるのだけれど、ここでも得意な人とそうでない人で差がつきそう。 漸化式が苦手な人はある程度集中的に勉強しておく必要があるね。 解説動画を見る

(1)は接線に関する基本中の基本問題。(2)は定積分で表された関数を求める問題で、最後の問以外は基本です。 最後の面積2等分問題はノーヒントだと結構難しいかもだけど直前のヒントを利用すれば一瞬。 解説動画を見る

教科書傍用問題集にありそうな問題です。角の二等分線の性質を使って辺の長さを求める問題。辺の長さを追いかけるか？ それとも面積を絡めて考えるか？どちらの解法もやっておきましょう。 解説動画を見る

重複順列で特定の2組の文字が隣り合わないものを求める問題。これ、意外と苦戦した人が多いのではないかな？キーワード「隣り合わない」のせいで解き方を決めつけてしまうとドツボにはまるのですよ。 それ以外にも余事象を数えるなど もちろん最初から方針がうまく立った人はほぼ一瞬なのだが、勉強すべきはそこではないと思うのですよ。最初の一手がうまくいかないときの軌道修正ができるかどうか？これが本番でもっとも大切。 この問題で何を学ぶのか、お間違いなく うまくいかないとき、まず考えるべきは基本にかえること。実験できるなら適当な値をつかって様子を見ることが大切。 そこから何か法則性が見えてくることは多いです。 解説動画を見る

これは簡単ですよね。 対称式の処理をスムーズに行えるように練習することはお忘れなく！ 解説動画を見る

さあ、明治大学に入りました！なんの変哲もない空間の位置ベクトルを求める問題ですが、案外計算がぐちゃぐちゃになってミスる人がいると予想。 すっきりした計算方法とは？というお話です 解説動画を見る

お馴染みの余りを求める問題。(1)(2)は教科書の例題と同じでしょ。(3)は2重因子を含んだ式で割った余りで少し難しい。もちろん扱い方を知っている人なら「いつもの問題」 という感じか。数Ⅲまでやっていれば微分する手もある。 それにしても自分が高校生だった頃はこんなに親切な説明は参考書には書いてなかったなあ。 　　　　P(x)を(x+1)^2で割った余りはs(x+1)^2+3x+2と表せる。 なんていきなり書いてあった。さっぱりわからなかった。 解説動画を見る

恥ずかしながら、最初三角比を使って問題を解きました。その後で見直して愕然！な、なんなんだコ、 コレは…幾何の性質だけで考えた方が百倍簡単じゃないか？久しぶりに平面幾何の威力を認識したのでした。
方べきの定理や接弦定理などは感が鈍っていると気付きにくいもの。定期的にこの手の問題をやって感を鈍らせないようにしないとね。 (3)は(1)(2)ができた人向けのボーナス問題。差の開く問題になってるなあ。こわい。
解説動画を見る

条件付き確率の典型的な問題です。が、同じ問題のはずなのに難しく感じた人が多かったのではないか？その要因は確率が文字で与えられていること。 その文字の表しているものが直感的に立式の時にリンクしてこないことではなかろうか。
わかりやすくするためには、言葉でその隙間を埋めていくことだ。事象をちゃんと書き出してみる。求めるべき確率を言葉で表現してみること。 こういう地道なことをやっていけば迷うこと無く正解にたどり着けるだろう。
最後の大小比較はとてもいい問題です。差をとることしかできない人は苦労する。 少し工夫してみようと思うことがとても大切だと気付かせてくれる問題です。
解説動画を見る

空間内に２つの円があってその円周上に4点をとって正四面体を作るという話。これが意外と複雑な状況で、 うまくまとめていくのは至難の業となります。それだけに(1)の正三角形の話はなんとしても正解したい。
細かいところまで詰めていくには時間がなさ過ぎるので本番ではかなり大まかな議論でなんとか答だけは出したい。 ただし解説は正確にやってますのでご安心ください。
解説動画を見る

与えられた定義の意味を深く考えず、なんとなく解いていっても正解が出せてしまった人はそれで満足してはいけませんよ。 この定義の意味を理解するには3桁の整数の大小を判断する方法と比較するとわかりやすいです。
解説動画を見る

3次関数のグラフを原点中心にθ回転とはヤバい問題だ。それがx軸と異なる３点で交わるようにしろといわれただけで焦るよね。 図を描こうにも３次関数のグラフを回転させた図をうまく描くのはけっこう大変だ。
もちろん３次関数のグラフを回転などさせてはいけない。それは出題者の罠だ。グラフをθ回転する代わりにｘ軸を-θ回転させてやればいいのだ。 x軸をθ回転すると傾きtanθとなる…なんて考え始めると話が難しくなる。
単純にy=mxとでもおいて面積をmで表すことにすれば話はスムーズに進むんだが、 そういう臨機応変が試験会場でできるかどうか？そう考えるとやっぱり難しい問題なんだよねえ。しっかり解説します！
解説動画を見る

福田のアプリ・首都圏有名私大入試問題解説がアップデートされました。
2022年度入試の早稲田大学が完成しました。これで早慶は完了です。 あわせて過去4年間の問題、解答、解説が利用できます。

早稲田商学部はここからが本番！難問揃いは今年も同じでしたね。特にこの問は理工学部の大問３と同類の考え方をする問題ですが、 なんと、理工学部の問題よりも難しいときた。もちろん本番では触らぬ神に祟りなしです。
しかし、勉強する人は参考になることも多いのでやっておくべき。この問に答えるためには漸化式で与えられた数列 もちろんその漸化式は解けない場合）がどんな値をとるのかをxy平面上で可視化できるか？が問われる
その方法なら知ってるよ、って言う人はなかなかの数学マニア。でもこの問題、それを知っていても、なお難しいのです。 可視化の方法を丁寧に説明してから、さらなる考え方についても解説します。
解説動画を見る

対称式っぽい問題ですが微妙に対称式になっていない問題です。でも変数を置き換えることで完全な対称式になるので解決していく問題です。 後は対称式の扱いをちゃんとわかっているかどうかが問われます。
解説動画を見る

漸化式を解く問題です。両辺の対数をとることで解ける形にもっていくタイプですが、２回連続で対数をとる必要があるのが新しいところです。 ただ、両辺の対数をとるときに注意すべきことがあるのでそれを解説しました。
解説動画を見る

3次関数が極値をもつ条件、３次方程式が異なる３個の実数解をもつ条件など、登場する条件はお馴染みのものですが、 それが組み合わさって結構複雑に感じるかも。大切なのは大きな流れを見落とさないことです。
解説動画を見る

(1)は簡単。(2)のD2をどうやって求めるか？２通りの解法を紹介しました。ポイントは三角形の外接円の半径を求めればよいと言うこと。 外接円の中心を求めるか？正弦定理で半径を求めるか？
結論から言うと正弦定理が圧倒的に楽だ。でも解く前にそれを予想するのは難しい。 受験本番では最適な方法を選べるかどうかわからない。そんなときでも（少々下手でも）やりきることは大切。
何が言いたいかというと、うまい解法ばかりじゃなくて、色々やってみるってこと。最後の最大最小については答案がうまく書けない人が多いよ。 結論だけで満足せずその過程を書けるようにしておこう。
解説動画を見る

状況把握がしっかりできるかどうかが問われる問題。あわてずに慎重に考えねばならない。n回サイコロを投げて出た目の積が3個の約数をもつ確率、 4個の約数をもつ確率を求める問題。どんな出方をするときなのか？
まずは約数の個数を求める方法が身についているかが問わる。約数の個数が3個になるのはサイコロの目の積がp^2となるときだけであることが結論できるかどうか。 となるとn回投げたサイコロの目の積が2^2, 3^2, 5^2しかない。
ここで細かい話が登場する。nが1のときは特殊な状況なので分けて話をする必要があるということ。「n回投げて」という問題文からして、さすがに「1回しか投げない」なんてことはないっしょ。 と言いたくなるが可能性のある限り調べなくては。
高校生に指導するときどうするか？最初から細かい話を要求せず大筋だけを考えさせるという指導方法はアリだとは思うけれど、 先生方はどうされているのかな？最初から細かいところまで押さえさせるのがいいのか、それとも…悩ましい。
もちろん受験の頃には細かい議論ができるようにしておかないと。そこでしっかり場合分けした解答を用意しました。
解説動画を見る

部分分数分解による無限級数の和を求める問題、ということはすぐにわかるね。ただ分母に4つの因数があるので簡単にはいかないという問題。 効率的に分解するにはどうすればよいか？さあ考えましょう。
解説動画を見る

四面体２個の共通部分を平面で切った切り口の面積を求める問題。空間思考が苦手な人もこの問題を嫌がらず考えるようにね。 「共通部分を切る」と考えると難しいが、「それぞれの切り口の共通部分」と考えることで簡単になります。
四面体を切るなら（底面に平行な平面で切るだけだから）切り口はすぐわかります。シンプルに考えられるコツを解説します。 ポイントは相似比を考えることだと思いますよ。座標計算を入れると面倒になります。
解説動画を見る

定積分で表された関数の問題。同種の問題は頻出ですが、その中でも結構複雑な式が与えられています。 ポイントになるのは絶対値の処理です。ここさえ乗り越えられれば解決は近いぞよ。
解説動画を見る

空間ベクトルの問題です。幾何的発想と代数学的発想の両方を紹介しています。条件が 内積が0 なので、ここから 直角 →　　直径の作る円周角は９０度 とつなげることで図形的な発想ができますね。
あるいは単にx, y, zに関する条件をたてて、 (x-2)^2+y^2+z^2 の最大を考える問題として文字式の処理をする発想。 シュワルツの不等式を持ち出して、徹底的に計算のみで解く方法を紹介しましたよ。
解説動画を見る

複素数平面上の点の軌跡を考える問題。求める点をx+yiとおく方法は通常推奨されないことが多いけれど、これが解きやすいときもありますよ。 この問題の条件は複素数の実部と虚部に条件が付いているのでx+yiとおくのと相性がいいね。
そんなことばかりやっていると複素数の力が付かないから、やっぱり教える側とすれば複素数の強力な性質を活かすような解き方を推奨。 ま、受験会場では解きやすい方で、勉強するときは両方しっかり！が正解かな。
解説動画を見る

楕円と接線が接する条件は簡単。後は回転体の体積ですが、これも教科書の例題にありそうな問題。 ただ、外周りの立体の体積から内回りの立体の体積を除く処理が確実にできるかどうか、計算力も必要です。
解説動画を見る

２次関数の最大最小問題の典型的な問題。幅が2の区間における最大値、最小値問題です。軸と区間の位置で場合分けするやつですね。 これは迷うことは無いはず。計算ミスをしなければ満点がとれます。
解説動画を見る

3変数a,b,cに関する問題。与えられた式がすべて対称式であることに注目です。まず最初に考えるべきことは1変数切り離して2変数の対称式と考えるべきか？ あくまで3変数の対称式として処理すべきか？ということ。
その判断は何を問われているかによって変わります。問われているのがcについての性質だったら、これは２変数a,bの対称式と見る方がよい。 しかしこの問題で問われているのはa,b,c均等の性質だから、3変数のままがよさそう。
さて３変数の対称式を扱う方法の重要な考え方に３次方程式の解と係数の関係を用いるというのがあります。 この考え方を用いることでa,b,cを3次方程式の解と見なせるのでグラフ利用するなど、考え方が広がりますね！
解説動画を見る

面対称な点を求め、その後で折れ線の長さの最小となる折り返しポイントを求める、よくある問題です。 特に平面図形で折れ線の最小を求める問題が頻出です。 その空間バージョンの問題。問題文から流れをつかむことが大切。
面対称な点の求め方を色々解説しました。折れ線の最小は「答えは求められるけど説明が下手で…」という人も多いでしょう。 答案の書き方も説明してますので記述力を養成してね。
解説動画を見る

三角不等式のごちゃごちゃした問題。角がθ、2θ、3θと混ざっているのでまずはこれを処理すること。 今回の解説では2倍角、3倍角の公式を使ってすべてをθで統一するという手順を踏みました。
他の発想としては 2sinθ+2sin3θ の部分に和を積になおす公式を適用する方法もありますよ。そしたら sin2θが共通因数になって因数分解ができてしまいますね。 最後のポイントはsinθ>0であることを忘れないこと。
解説動画を見る

辺の長さに関する関係式から三角関数の値を求める問題です。こういう問題をパズルのように色々やり、 偶然うまくいってしまうような解答をしていると数学の力はついていきません。 （色々やってみることを否定しているわけではありません)
色々試すことはとても大切ですが、闇雲にやるだけではなく、 ・この問題に使える道具は何か？ ・求めるべきものは何か？ を考えてみましょう。使うべき公式も見えてくると思います。
解説動画を見る

頂点が第１象限または第３象限にある条件をちゃんと立式できればおしまいですね。 あとは解の個数を数えるところでミスることも考えられるので油断大敵！
解説動画を見る

論理パズルの問題として、いいんじゃないですかね。もしかししてどこかのパズル本になかったでしたっけ？ ある命題の真偽をできるだけ少ない手数で判定する方法を考えさせる今年の早稲田の会心作？
これ、見事に引っかかってしまったけど恥かしくて誰にも言ってない人以外と多いんちゃう？なんとなくできてしまったけど深く考えていない人も多いかも。 この問題は命題の逆は必ずしも真ではなく、命題の対偶は…
解説動画を見る

2022年の早稲田理工学部の問題セットで一番素直な問題でしょう。なんとか得点しておきたいね。
だからといって簡単とは言えない数Ⅲらしい難しさもあります。特に(3)は条件を求めるのに下手な計算をすると大変になるし、条件が求まったとしてもそれを図示するところで面倒な計算が必要になる。 つまり時間がかかる。
だからこそ、第１問の超大変な計算が響いてきそうだなあ。
解説動画を見る

正八面体の1つの頂点を頂点とする正四角錐をピラミッドと呼ぶことにします。 正八面体には６個の頂点があるので６個のピラミッドを考えることができます。 その６個に内接する球がB_1～B_6なんです。ここまでを理解するが大変でした。
隣どうしの球B_1とB_2の和集合の体積、B_1,B_2,B_3の体積を求める所までは集合の要素を数える公式で簡単にでてきます。 が、 6個の球すべての和集合の体積となると状況は一気に複雑になりますね。さて、どうするか？
6個の球の位置関係をまともに考える方法もありますが、話を単純にする工夫が入試問題を解くときにはとても大切です。 今回の解説ではこの部分が最大の見せ場です。その後の問はごく普通の問題なんだよね。
解説動画を見る

ガウス記号を含んだ漸化式で定義された数列の極限を求める問題です。 (1)(2)の流れから「はさみうちの原理」が予想されるのだが… 入試問題でよくあるパターンを裏切る問題ですねえ。
よくあるパターンとはガウス記号の定義から、すぐ導ける性質 x-1<[x]≦x を用いて、はさみうちの原理で極限を求めるというもの。 はさむことはできるのだが、その両端が同じ値に収束しないので撃沈！
ここで、発想を転換できる人は受験に強い人。 ひとつの考えに固執していては光は見えてこないのです。 別の解決策として２つの方法が見えてきます。
一つ目は予想して、そこからヒントを得る方法。特性方程式を解いてみれば極限値の予想はできる。 もう一つはグラフを利用して極限を視覚化すること。 二つ目の方法は発展学習ではあるものの有名な方法です。
ガウス記号を含んだグラフを描いたことは誰しもあるはず。それがこんなところで役に立つとは！ 漸化式を関数と考えてグラフを描き、そこから極限を眺める方法を動画では詳しく解説しています。 是非ご覧ください。
解説動画を見る

関数の係数決定問題と整数の約数倍数の関係をうまく結びつけた問題でした。 解の総和については2m次方程式の解と係数の関係を使うのかと思ったけれど、 全部の解が求まってしまうのね。つまんない…
解説動画を見る

これは… 問題はよくあるグラフ描画 → 面積 → 回転体の体積 という見慣れた形式です。が！ 体積計算が…あまりに大変すぎないか？ 悩ましい、悩ましいぞ、これは。 計算さえ頑張れば得点はできる。
しかし、時間との駆け引きはどうなの？ 頑張った、時間もかけた、計算ミスでした。
なんてことになったら… あるいはそう思っているのは私だけ？
今の高校生はこのくらいの計算はへっちゃら？
それにしても出題者の心遣いも伝わってくる問題です。 少しでも計算しやすくするために積分区間になる交点の値がきれいにlog2, log3, log4, log6のように美しく並ぶんですね。
確かに計算しやすいけれど…
早稲田大学に是非正答率を教えて頂きたい。 正答率が3割を超えていれば今の高校生の計算力はかなり高いと見る。 もちろん部分点を取った人は多かったと思うので、 あくまでも完答した人の率を知りたい。
解説動画を見る

　f(x)がわからなくてもf'(x)さえわかっていたら∫f(x)dxの定積分が計算できるという話。 部分積分に気付けばある意味簡単な問題です。これは得点源にしないとね。 この問題の評価は

• 難易度★★★☆☆
• 計算量★★★☆☆
• 発想力★★★☆☆

　問題文を読んで「反射」だから放物線の性質から反射した直線が焦点を 通過するということに気付いた人はえらいと思います。 ま、「反射」を考えず、角の二等分線の傾きから直線の傾きを求めれば解けますね。 (3)は焦点を通過した直線が放物線で反射する直線を求める問題。 今度は焦点を使えないので計算するしかないと動画では説明しましたが、 もしかしたら(1)(2)から最初に入ってきた軸に平行な光線に平行になることを証明できそうだなあ。 この問題の評価は

• 難易度★★★☆☆
• 計算量★★★☆☆
• 発想力★★★☆☆

　第１問は去年に続き難しかったなあ。数え上げるだけである程度点が取れるようになっているので救われるけれど、 (4)が解けた人はほとんどいなかったのでは？ それでも(4)も答だけはなんとか出せたよ！って言う人もいたと思います。素晴らしいですね。 どういう採点基準で採点されたかはわからないけれど、 ある程度おおまかでも正しい結論を出せた答案にはたくさん点を上げて欲しい。 昨日から東京医科歯科大学2022年の解説動画を公開し始めました。 どの問題も骨のある重厚な問題です。是非挑戦してみてください！第１問はこちら。 解説動画を見る

　あれ？やけに簡単そうだぞ？と一瞬勘違いしそうな問題です。 ところがどっこい、やり始めると「当たり前だけどどう説明していいかわからない」となる問題です。 まさか、「グラフより明らか」で済まされるわけないしねえ。 (2)の方がある意味方針が立てやすいね。 ２つの図形の面積が等しくなるような条件を考えるので、とりあえず2つの面積を立式することは誰でもわかる。 だけど、ここに計算の大変さと制限時間の壁が立ちはだかることになるのでした。 結局(2)も撃沈！となりそう (1)をうまく説明できる人はグラフを色々描きながらあることを発見できる観察力のある人でしょう。 それは「３点で交わるようにするには傾きをできるだけ大きくとることなんだ」ということに気づけるかどうかです。 グラフを1、2個しか描かない人は気づけない (2)は面積が等しくなるのは、「原点を通る直線を引いたときだけ」ということに気づけば、 それを言葉でうまく言いくるめちゃえば部分点くらいはどれそう。 詳しくは以下のURLから解説動画をご覧ください。 解説動画を見る

　さすが東大！と思ってしまういい問題です。難しいだけの問題は山ほどあるけれど東大の問題が優れていると感じるのは、 よくよく考えると実は簡単だと気付かせてくれるときが多いのよね。 作問をする側の人間からしたら、そういう問題を作るのは至難の業。 東大さん、さすがです。この問題、まずは「十分に離れている」という状態の定義を与えてあって受験生はまずそれを理解することに全力を傾けることになる。 それさえ乗り越えられれば… そして補集合を考えることで考えやすくなることに気付くとトントン拍子に解決していくという過程を踏んでいくのだ。 素晴らしいね。 しかも場合分けに気付く必要もあるしね。解いていてだんだん楽しくなりそうです。 優しいけれど難しい。これが東大の数学の本質かな？この問題の解説動画は以下のURLからご覧くださいね！ 解説動画を見る

　これは難問だ。(1)は別として(2)から後は問題の意味がわからないと思う。a_n が a_kの倍数になるってどういうこと？ a_n も a_k も一般項だよね？どっちも動くの？ どっちかは定数なの？はっきりしないよね？ ヒントが無さ過ぎ問題発生なのよ。そのあとの問題文も「となるようなnをkで表せ」 のように書いてくれてあればまだ気付きやすいんだが… 「k, nを用いて表せ」とは意地悪にも程が過ぎるよ、まったく(--;) 実際にはkを固定して、つまりa_kを固定してa_kの倍数となる項が何番目にあるのか （それがn）を調べなさいということなんだ。それに気付くまでに高校生は苦労すると思うのよ。それがわかって始めて、 どんな実験をするべきかがわかってくるので 「実験しないから気付かないんだよ」とえらそうに言っても、高校生からしてみれば「？」なんだと思う。 まあそれくらい難しい問題だと言うこと。 私の解説動画はその実験を詳しく説明しているので興味があれば見に来てください。 解説動画を見る

　今年の東京大学の理系第１問は単なる計算問題でした。 昨年の第１問が歴史に残る印象深い問題でしたから、それと比べるとなんとつまらない問題なのか？ と思った人も多かったかも。 でも東大はよくこの手の問題を出すのよ。 ちなみに昨年2021年東大理系第１問は歴史に残る１題となりましたよ。 どんな問題か振り返りたい人のために詳しく解説した動画のリンク張ります。 ということで、今年の第１問は単なる計算問題。東大は単なる計算問題をよく出題するけれど、 これも東大のはなつメッセージと考えてよいのではないか？ 数学のひとつの側面として確かな計算力が必要なのだと言っているんだろうね とは言っても以外と計算に苦しんだ人もいたかもね。東京大学2022年理系数学第１問の解説動画はこちらです 解説動画を見る

　媒介変数表示で表された曲線の性質を説明してグラフを描く問題。 (1)(2)までは標準的なレベルだけど(3)からは厳しい。 だいたい多くの高校生が媒介変数表示のグラフの対称性を説明できないと思われ、 経験値がものを言う問題かも。 さらに曲線上の点を６０°回転した点がまた曲線上にあることを示す話は やっぱり複素数平面にもっていくんだろうなあ。臨機応変に立ち回れるか？これも厳しいねえ。 しかもその後の計算も相当むずいし 実はこの問題、慣れた人が見れば一発で内サイクロイド曲線とわかるはず。 原点中心半径6の円に内接する半径1の円が転がってできる曲線（内サイクロイド）なんだよね。 それを説明できるなら答案はかなりショートカットして楽もできますけどね。動画公開は5月8日 内サイクロイド（ハイポサイクロイドもしくはアステロイドともいう） 解説動画を見る 曲線の観点でこの問題を考える動画を別仕立てで作ったのでこれもアップしますよ。 ５月10日公開ですよ(^^)/~ 解説動画を見る

　長文、長文、長文ああ読む気がしない…というような問題です。しかもテーマが区分求積なのでややこしいったら。 でも断言できます。今年の九大の理系問題はこれが一番優しい問題だったと。 「え？これが？」と思う人もいるとは思いますが、答は「Yes」なのよ。 だからといって簡単とも言えない。定積分の定義を与えておいて、 そこから区分求積を説明させるという論証能力が必要な問題。 ある種の間違った受験勉強をしてきた人は帰ってねと言わんばかりの問題。 そういう意味では良問ですが、他の問題が超むずかったから… 今年同じことを感じたのが東工大だね。どちらも超難化です。 ちなみに九大のこの問題の解説動画は5月7日公開の予定です。お楽しみに! 解説動画を見る

　(1)(2)はごく普通の約数、倍数の整数問題。 (3)はひとつ見つけて!と言っているので適当に探してまぐれ当たりでもいいってことですね？ って思ってテキトーに代入しまくっても答が出てこないのですよ。 で、どうするか？となるので①の式をもっと単純化して値を見つけやすくする努力をしろってことです。 まあ(2)の結果を使うのは目に見えてますのでなんとかなるとは思います。（試験場でなんとかなるとは言っていない） ちなみにコンピュータを使って①に値を代入しても満たす解が見つからないのよ、 これが…これって満たす自然数の組が1つしかないってこと？ それともかなりでかい数になると見つかるのか？どうやってこんな方程式作った？九大恐るべし! 解説動画を見る

　(1)(2)も簡単ではないけど、(3)はどうだろう？予備校の解答を見ると微分の定義式にもっていっているけど 高校生がこの式を見て微分の定義式にもっていくか？そりゃ無理でしょ。 ということで猛烈に反発意識が高まったので普通に極限計算した結果をアップします。 あ、アプしますが、順番があるので５月５日にアプの予定です。少しお待ちを！ それにしても難しいな、今年の九大は！この後も難問揃いだぞ。 受験生が落ち込まなかったか心配。出題者はもう少し考えて欲しい。 解説動画を見る

　今年の九州大学の数学は難しくなったなあ( ; _ ; )/~~~ 九州大学の数学Ⅲの第1問は予備校の評価が「標準」になってるけど、そうか？簡単そうでむずいよ？ 平面に対して、2点が同じ側にあることなんて高校生にとっては簡単に説明できないと思うけどねえ。 予備校の解答を見ると内積を使ってしれっと説明してるけど、そんな発想出てくるとは思えないんだけど。 平面の方程式を利用できれば簡単なんだが。やっぱり高校生には平面の方程式は知っておいてほしいと思った今日この頃でした。 解説動画を見る

　高校へ入学された皆さん、いよいよ新しい生活が始まります。希望と不安の入り交じった気持ちでおられるのではないでしょうか。 私からは、皆さんへのメッセージとして、3回目の「わかった」を目指そうという話しをしたいと思います。高校生になって一番の不安は勉強の事だと思います。中学と違って内容が難しくなるので、自分はついていけるのだろうか？ と思ってしまいますよね。特に心配なのは数学ではないでしょうか？ そこで高校数学を学ぶ上で知っておいて欲しいことをお話しします。

　それが3回目の「わかった」を目指そうという話しです。中学数学と比べると高校数学はかなり難しくなります。1回「わかった」と思っても、しばらくすると 「何も分かっていなかったんじゃあないか？」と思うことが結構あるんです。中学の時だったら、 1回理解してしまえば、それで大丈夫だったことが 高校ではそうではなくなるのです。そこで3回目の「わかった」を目指そうという話しになります。

　まず1回目の「わかった」を味わ必要がありますよね。 できることなら、その瞬間は教室の中であるべきです。そのために、是非予習に力を入れて下さい。 予習することで明日受ける授業の内容に疑問点が見つかります。 その疑問点を、授業で解決するのです。先生がどう説明してくれるのか、授業も楽しみになりますね。 もしその疑問点を先生が明確に話してくれなければ、直ぐに質問に行きましょう。こうすることで1回目の「わかった」をいち早く経験できます。

　ところがです。分かったつもりが分かっていないのですよ。 その後復習で問題を解いたり、定期テスト前に勉強し直したりすると、また疑問が出てくるのです。 高校数学ではそんなことが、頻繁にあります。それだけ奥が深いと言うことなんです。 分かったつもりの問題がわからない。そんな時は授業のノートを見直しましょう。 そこに、気になる事が書いてありませんか？できることなら記憶を辿り、先生がその時、授業で何を喋っていたか、思い出して下さい。 先生は生徒が陥りがちな部分をよく知っているので授業で、その話しをしてくれていた可能性は高いです。 ただ、その時あなたは、まだそこまでの理解度に達していなかったのでその話の真意を知ることが出来なかったのでしょう。この「わかったつもりが、わかっていなかった」ことに気付いたときがチャンスなんです。自分一人で乗り越えられなかったら、躊躇せずに質問に行くべきです。こうやってあなたは2回目の「わかった」を経験できます。そして、また一段レベルアップしていけるのです。

　じゃあ3回目の「わかった」は何なの？と思いますよね。3回目の「わかった」は実はずっと後に訪れます。3年生になって入試問題を解くようになったとき、それまで皆さんは、分野ごとのセパレートコースを走っていたのです。それが3年生になると、オープンコースに変わります。つまり、今までやってきた分野が入り交じって融合問題を解く事になります。その時になって、またわからなくなるのです。今まで関係が無いと思っていた違う分野との関係を問われた時、初めてあの時習った事柄の本当の意味に気付かされるのです。点と点が結ばれて線になる瞬間ですね。ここまでできら、あなたの知識は完全に活きたものとなるのです。でも慌てないで。それはずっと先の話です。まずは1回目の「わかった」に向けて予習をしていきましょう。3回目の「わかった」を目指して。

　答を見ても賢くならない。数学を勉強する上で心に留めておくことです。 どんなに丁寧な解説を読んでも、それだけであなたの数学力が向上するわけでわありません。 何度繰り返し読んで暗記しても、いざ問題を解こうとするといい考えが浮かんでこない。 なぜなのか？ 問題を解くときの状況を想像して下さい。

　私たちは問題を解くときに思考の森に入っていきます。その森はいくつもの道に枝分かれし正解というゴールに つながっている道はほんの少ししかありません。 しかもその道は枯れ葉などで隠されいるのかもしれないのです。 そんな状況で私たちは正しい道を見つけださなければなりません。思考の森のイメージをご覧下さい。まず問題があります。 初見で3通りの着想があったとしましょう。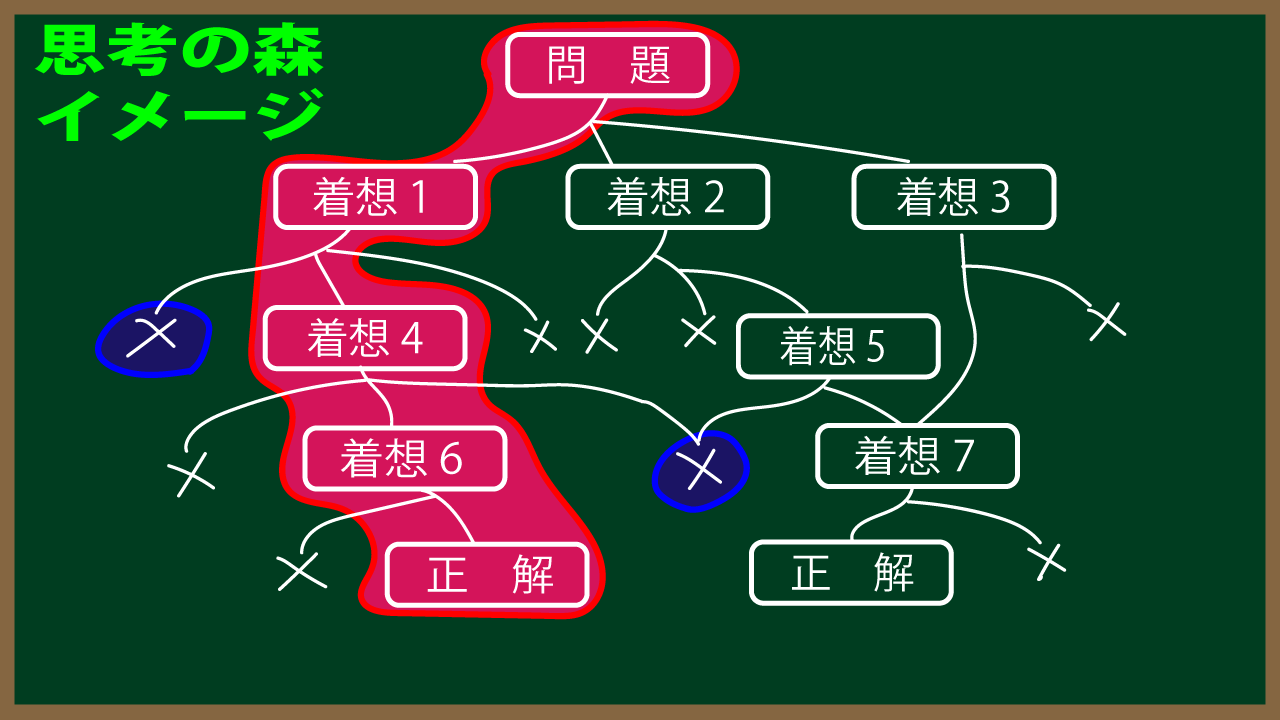

　A君は着想1を選びました。しかしそのアプローチには3つの方法があり、そのうち2つは失敗します。 A君はなんとか着想4へたどり着きました。ここでもまた、3つのアプローチがあってその中で有効な方法は1つだけです。 その方法なら後の処理を誤らなければ正解にたどり着けます。

　B君は最初の段階で着想2を解き始めました。その後だめな道を選ぶことなく着想5へたどり着き着想7 へとつなげることで正解に到達出来ました。

　C君は着想3に気付きました。かなり斬新な発想です。 この方法だと着想5を飛ばして一気に着想7へ飛んで行けて正解にたどり着けます。 しかし多くの人がこの森で道を間違えて×のところで立ち往生してしまいます。

　また来た道を戻ってやり直すのですが、なかなか正しい道が見えてきません。そこで参考書のお世話になるわけです。 しかし参考書には何が書かれているのでしょうか。参考書に書かれているのは、 おそらく今色を付けたこの部分の説明なんです。 あるいは、別解答としてこの解法も書いてくれている参考書もあるでしょう。

　そしてその内容は各ステップを事細かに丁寧に説明してくれていると思います。 それを読めば正しい道の確認はできますが、だからと言って、それで思考の森で迷子にならないわけでわないですよね。

　私たちが必要としているのは道に迷ったとき、あるいは迷いそうなときに、どうやって正しい道を選択するのか、 その知恵であり判断力です。

　たとえば今青く塗ったこの間違いについて解説してほしいと思いませんか？ さらにもう1個青く塗った×、 これは2つの着想からどちらからでも陥る共通の間違いなので多くの人が踏み入ってしまいそうな所だと思われます。 こんな所の話も聞いてみたいでしょう。 でも残念ながら参考書にはそのことはほとんど書かれていません。なぜなら、本当の思考の森はこの図よりも はるかに複雑なので、すべてをカバーする事は難しいのです。 そこまで事細かに書かれた文などとても読み切れないでしょう。

　私たちが数学を賢くなるには参考書を読むだけでは十分ではありません。 思考の森の中で自然に正しい道を選んでいける「コツ」をつかむ必要があります。

　A君は同じ分岐点で、何の迷いもなく正しい道を選びます。なのに自分は間違った道を選んでしまう。 「なぜ自分は正しい道を選ばなかったのか？」 「なぜ自分はいつも間違った道を選んでしまうのか？」 その答えを探す必要があります。そこに自分の足りないものがあるのでしょう。 そしてその答は参考書には書いてないのです。

　ではどうすればよいのか？ まず問題を整理しておきましょう 分岐点において、間違った道を選んでしまう状況として

1. そもそもそんな道があることを知らなかった。
2. その道があまりにも大変そうだったので楽な道を選んでしまった。
3. その道も頭をかすめたが、別の道の方がよいと思った。

　このうち、1のタイプの人は明らかに経験不足。対処方法は「もっと勉強しなさい」という当たり前の 話しなのでこれから期待ですね。

　2のタイプの人は「うまい解法」にこだわりすぎる人が多いです。 たとえば、場合の数の問題ですべて書き出せば終わるのに面倒くさがって 計算でなんとかしようとして自爆するタイプ。 大切な計算や作業でも正解に辿り着けるならその道を行くべきですよね。

　そして3のタイプ。この人が一番問題なんです。 自分の考えにこだわりすぎる人に多い状況です。 そして新しいことをなかなか受けいることができない人に多い状況です。 数学が得意な人に多い状況です。 なまじっかできる人なので、自分の方法から脱却できないのです。

　あなたは大丈夫ですか？ 問題を解きました。解答を見て答があっていました。 解説を読むと自分の解いた方法ではないことが書いてあります。 読んでみたが、なんかすっと頭に入ってこない。 でもできたからいいじゃないか。 となって終わってしまう人、結構多いです。 こういう人は進歩するチャンスを自ら放棄してしまっているのです。

　自分の理解できないことが解説に書いてあったなら、 おそらくそこには自分の知らなかった「ある事柄」が隠されているんです。 その事柄を知ることで今まで分かっていなかった問題が解けるようになるかもしれません。 解けたんだから、それでいいじゃないかと思って新たな知識を遮断すると、 その知識が必要な問題に出くわしたときに 正しい道を選ぶことができなくなります。 結局たくさん勉強してきても「知らないこと」は存在するのです。 私自身、40年以上も受験数学を指導してきましたが、 今でも「こんな方法があるんだ!」という事が常にあります。 高校生の段階ですべて知っているなんてあり得ないのです。

　A君は分岐点でなんの迷いもなく正しい道を選んでいきます。 なのに自分は間違った道の方を選んでしまう。 それはA君が知っていて、君が知らない何かがあるからです。 多分A君が天才だからではありません。

　ですから思考の森で迷子になったら次のように考えましょう。 ある事柄を自分は知らない。その事柄を理解していれば、自然に正しい道を進みたくなるようになるはず。 でも参考書にそこまでは書いてないので「自分の知らない事柄がなんなのか？」がわかりません。 そんなときは、身近にいる先生や友人に聞いてみるのがいいでしょう。

「自分はこの問題でここまで、できたんですが、この後こう進んで、結局解けませんでした。」 というような聞き方をしましょう。 そうすれば「え、こんな考え方は知らないかな？」みたいな解答が返ってくるかもしれません。 そうなったらしめたものです。けっして「この問題が解けません。教えて下さい。」などと言う聞き方はしないことです。 その質問の答えは参考書の解説と同じになってしまいますから。